Tim Randolph

Theory of Computing (ToC) is an important aspect of nearly every undergraduate CS curriculum, as it concerns what computation fundamentally means. However, there has been little research into ToC pedagogy, both within the classroom and how it fits within its institutional context. We propose in this working group to create a survey of current ToC pedagogy. Our goals are to create a standard for teaching ToC, find trends, determine under-researched areas, and to build a community among ToC educators.

We study the parameterized complexity of algorithmic problems whose input is an integer set A in terms of the doubling constant \(C:=|A+A|/|A|\), a fundamental measure of additive structure. We present evidence that this new parameterization is algorithmically useful in the form of new results for two difficult, well-studied problems: Integer Programming and Subset Sum.

First, we show that determining the feasibility of bounded Integer Programs is a tractable problem when parameterized in the doubling constant. Specifically, we prove that the feasibility of an integer program I with n polynomially-bounded variables and m constraints can be determined in time \(n^{O_C(1)} poly(|I|)\) when the column set of the constraint matrix has doubling constant C.

Second, we show that the Subset Sum and Unbounded Subset Sum problems can be solved in time \(n^{O_C(1)}\) and \(n^{O_C(\log \log \log n)}\), respectively, where the \(O_C\) notation hides functions that depend only on the doubling constant C. We also show the equivalence of achieving an FPT algorithm for Subset Sum with bounded doubling and achieving a milestone result for the parameterized complexity of Box ILP. Finally, we design near-linear time algorithms for k-SUM as well as tight lower bounds for 4-SUM and nearly tight lower bounds for k-SUM, under the k-SUM conjecture. Several of our results rely on a new proof that Freiman's Theorem, a central result in additive combinatorics, can be made efficiently constructive.

We present a variety of exact and parameterized algorithms for Subset Sum and other related problems. The major contributions of this thesis include:

• 1. Average-case algorithms for Generalized Subset Sum, the problem that generalizes both Subset Sum and Equal Subset Sum, as well as structural results describing the parameter regime in which solutions exist. These results extend the application of the "Representation Method" and are the fastest known in this setting.
• 2. A proof that Either-Or Subset Sum, the problem of solving either Subset Sum or Equal Subset Sum, can be solved exponentially faster than time \(2^{0.5n}\) in the worst case. In our view, this result illustrates the potential of the "structure vs. randomness" approach for Subset Sum.
• 3. Algorithms that solve worst-case Subset Sum faster than time \(2^{0.5n}\) by a polynomial factor. These improvements on the best known exact algorithms for Subset Sum represent the successful application of "log shaving" techniques to the problem.
• 4. Algorithms for Subset Sum and \(k\)-SUM with constant doubling. When considered in terms of a novel parameterization in the doubling constant, Subset Sum admits an XP-algorithm, while \(k\)-SUM is Fixed-Parameter Tractable. We also show that Subset Sum is FPT in the doubling constant if and only if an instance \(\mathcal{I}\) of Hyperplane-Constrained Integer Linear Programming with \(n\) variables, \(m\) constraints, and constraint matrix entries bounded by \(\Delta\) can be solved in time \(\Delta^{O(m)} \cdot poly(|\mathcal{I}|)\).

We implemented pedagogical strategies designed to give students greater control over the use of class time and grading methods in a major-required computer science theory (CST) course. Our methodology addresses the challenges inherent in transferring more power to students in a lecture-based class with a curriculum that requires the sequential mastery of formal mathematical concepts.

We offered students increased control over four classroom variables: the degree of interactivity, the selection of in-class activities , increased emphasis on standards-based outcomes as opposed to averaging over all coursework, and the granularity of the grading schema used by TAs. In this experience report, we present our methodology, report on our classroom experience, and conclude that increasing student control over the undergraduate CST classroom via participatory governance can increase student motivation and encourage critical reflection in budding computer scientists.

A subset S of the Boolean hypercube \(\mathbb{F}^n_2\) is a sumset if \( S=\{a+b:a,b \in A\}\) for some \(A \in \mathbb{F}^n_2\). Sumsets are central objects of study in additive combinatorics, featuring in several influential results. We prove a lower bound of \( \Omega(2^{n/2}) \) for the number of queries needed to test whether a Boolean function \( f : \mathbb{F}^n_2 \rightarrow \{0,1\} \) is the indicator function of a sumset. Our lower bound for testing sumsets follows from sharp bounds on the related problem of shift testing, which may be of independent interest. We also give a near-optimal \(2^{n/2} \cdot poly(n)\)-query algorithm for a smoothed analysis formulation of the sumset refutation problem.

A major goal in the area of exact exponential algorithms is to give an algorithm for the (worst-case) n-input Subset Sum problem that runs in time \(2^{(1/2−c)n}\) for some constant \(c>0\). In this paper we give a Subset Sum algorithm with worst-case running time \(O(2^{n/2⋅n−γ})\) for a constant \(γ>0.5023\) in standard word RAM or circuit RAM models. To the best of our knowledge, this is the first improvement on the classical "meet-in-the-middle" algorithm for worst-case Subset Sum, due to Horowitz and Sahni, which can be implemented in time \(O(2^{n/2})\) in these memory models.

Our algorithm combines a number of different techniques, including the "representation method" introduced by Howgrave-Graham and Joux and subsequent adaptations of the method in Austrin, Kaski, Koivisto, and Nederlof, and Nederlof and Wegrzycki, and "bit-packing" techniques used in the work of Baran, Demaine, and Patrascu on subquadratic algorithms for 3SUM.

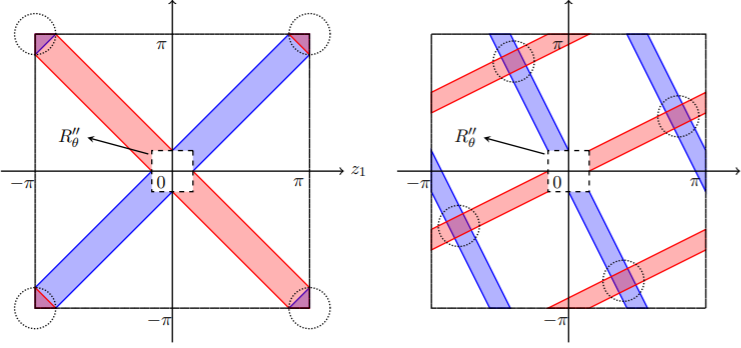
Given a set of \(n\) input integers, the Equal Subset Sum problem asks us to find two distinct subsets with the same sum. In this paper we present an algorithm that runs in time \(O^*(3^{0.387n})\) in the~average case, significantly improving over the \(O^*(3^{0.488n})\) running time of the best known worst-case algorithm and the Meet-in-the-Middle benchmark of \(O^*(3^{0.5n})\).

Our algorithm generalizes to a number of related problems, such as the Generalized Equal Subset Sum problem, which asks us to assign a coefficient \(c_i\) from a set \(C\) to each input number \(x_i\) such that \(\sum_{i} c_i x_i = 0\). Our algorithm for the average-case version of this problem runs in~time \(|C|^{(0.5-c_0/|C|)n}\) for some positive constant \(c_0\), whenever \(C=\{0, \pm 1, \dots, \pm d\}\) or \(\{\pm 1, \dots, \pm d\}\) for some positive integer \(d\) (with \(O^*(|C|^{0.45n})\) when \(|C|<10\)). Our results extend to the~problem of finding "nearly balanced" solutions in which the target is a not-too-large nonzero offset \(\tau\).

Our approach relies on new structural results that characterize the probability that \(\sum_{i} c_i x_i =\tau\) has a solution \(c \in C^n\) when \(x_i\)'s are chosen randomly; these results may be of independent interest. Our algorithm is inspired by the "representation technique" introduced by Howgrave-Graham and Joux. This requires several new ideas to overcome preprocessing hurdles that arise in the representation framework, as well as a novel application of dynamic programming in the solution recovery phase of the algorithm.

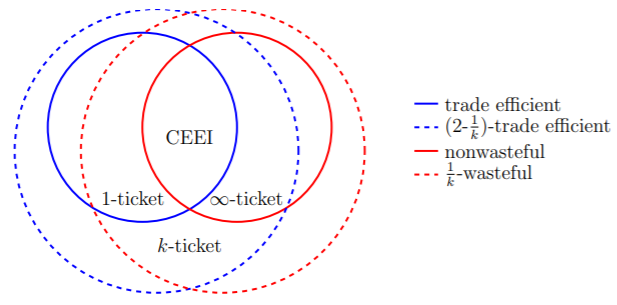
We analyze the \(k\)-ticket lottery, which is used to allocate hunting permits in the state of Alaska. Each participant is given \(k\) tickets to distribute among lotteries for different types of items. Participants who win multiple items receive their favorite, and new winners are drawn from the lotteries with unclaimed items.

When supply is scarce, equilibrium outcomes of the \(k\)-ticket lottery approximate a competitive equilibrium from equal incomes (CEEI), which is Pareto efficient. When supply is moderate, \(k\)-ticket lotteries exhibit two sources of inefficiency. First, some agents may benefit from trading probability shares. Second, outcomes may be "wasteful": agents may receive nothing even if acceptable items remain unallocated. We bound both sources of inefficiency, and show that each is eliminated by a suitable choice of \(k\): trades are never beneficial when \(k=1\), and waste is eliminated as \(k\) approaches infinity.

The wastefulness of the \(k\)-ticket lottery has some benefits: agents with strong preferences may prefer \(k\)-ticket lottery outcomes to those of any nonwasteful envy-free mechanism. These agents prefer small values of \(k\), while agents with weak preferences prefer large values of \(k\). Together, these results suggest that the \(k\)-ticket lottery performs well under most circumstances, and may be suitable for other settings where items are rationed.

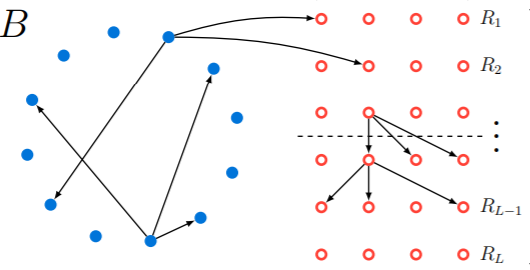
We consider the problem of finding a cycle in a sparse directed graph \(G\) that is promised to be far from acyclic, meaning that the smallest feedback arc set in \(G\) is large. We prove an information-theoretic lower bound, showing that for \(N\)-vertex graphs with constant outdegree any algorithm for this problem must make \(\tilde{\Omega}(N^{5/9})\) queries to an adjacency list representation of \(G\). In the language of property testing, our result is an \(\tilde{\Omega}(N^{5/9})\) lower bound on the query complexity of one-sided algorithms for testing whether sparse digraphs with constant outdegree are far from acyclic. This is the first improvement on the \(\tilde{\Omega}(\sqrt{N})\) lower bound, implicit in Bender and Ron, which follows from a simple birthday paradox argument.

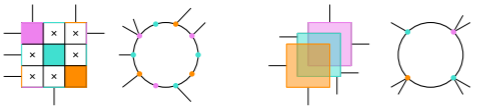
We present a new model for hybrid planarity that relaxes existing hybrid representations. A graph \(G=(V,E)\) is \((k,p)\)-planar if \(V\) can be partitioned into clusters of size at most \(k\) such that \(G\) admits a drawing where: (i) each cluster is associated with a closed, bounded planar region, called a cluster region; (ii) cluster regions are pairwise disjoint, (iii) each vertex \(v \in V\) is identified with at most \(p\) distinct points, called ports, on the boundary of its cluster region; (iv) each inter-cluster edge \((u,v)\in E\) is identified with a Jordan arc connecting a port of \(u\) to a port of \(v\); (v) inter-cluster edges do not cross or intersect cluster regions except at their endpoints. We first tightly bound the number of edges in a \((k,p)\)-planar graph with \(p<k\). We then prove that \((4,1)\)-planarity testing and \((2,2)\)-planarity testing are NP-complete problems. Finally, we prove that neither the class of \((2,2)\)-planar graphs nor the class of \(1\)-planar graphs contains the other, indicating that the \((k,p)\)-planar graphs are a large and novel class.

Let \(G=(V,E)\) be a graph and \(t,r\) be positive integers. The signal that a tower vertex \(T\) of signal strength \(t\) supplies to a vertex \(v\) is defined as \(sig(T,v)=max(t−dist(T,v),0)\), where \(dist(T,v)\) denotes the distance between the vertices \(v\) and \(T\). In 2015 Blessing, Insko, Johnson, and Mauretour defined a \((t,r)\) broadcast dominating set, or simply a \((t,r)\) broadcast, on \(G\) as a set \(T \subseteq V\) such that the sum of all signals received at each vertex \(v\in V\) from the set of towers \(T\) is at least \(r\). The \((t,r)\) broadcast domination number of a finite graph \(G\), denoted \(\gamma_{t,r}(G)\), is the minimum cardinality over all \((t,r)\) broadcasts for \(G\).

Recent research has focused on bounding the \((t,r)\) broadcast domination number for the \(m \times n\) grid graph \(G_{m,n}\). In 2014, Grez and Farina bounded the \(k\)-distance domination number for grid graphs, equivalent to bounding \(\gamma_{t,1}(G_{m,n})\). In 2015, Blessing et al. established bounds on \(\gamma_{2,2}(G_{m,n})\), \(\gamma_{3,2}(G_{m,n})\), and \(\gamma_{3,3}(G_{m,n})\). In this paper, we take the next step and provide a tight upper bound on \(\gamma_{t,2}(G_{m,n})\) for all \(t>2\). We also prove the conjecture of Blessing et al. that their bound on \(\gamma_{3,2}(G_{m,n})\) is tight for large values of \(m\) and \(n\).

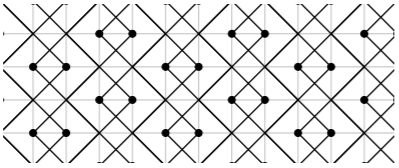
Let \(G=(V,E)\) be a graph and \(t,r\) be positive integers. The signal that a tower vertex \(T\) of signal strength \(t\) supplies to a vertex \(v\) is defined as \(sig(T,v)=max(t−dist(T,v),0)\), where \(dist(T,v)\) denotes the distance between the vertices \(v\) and \(T\). In 2015 Blessing, Insko, Johnson, and Mauretour defined a \((t,r)\) broadcast dominating set, or simply a \((t,r)\) broadcast, on \(G\) as a set \(T \subseteq V\) such that the sum of all signals received at each vertex \(v\in V\) from the set of towers \(T\) is at least \(r\). We say that \(T\) is optimal if \(|T|\) is minimal among all such sets \(T\). The cardinality of an optimal \((t,r)\) broadcast on a finite graph \(G\) is called the \((t,r)\) broadcast domination number of \(G\). The concept of \((t,r)\) broadcast domination generalizes the classical problem of domination on graphs. In fact, the \((2,1)\) broadcasts on a graph G are exactly the dominating sets of \(G\).

In their paper, Blessing et al. considered \((t,r) \in \{(2,2),(3,1),(3,2),(3,3)\}\) and gave optimal \((t,r)\) broadcasts on \(G_{m,n}\), the grid graph of dimension \(m\times n\), for small values of \(m\) and \(n\). They also provided upper bounds on the optimal \((t,r)\) broadcast numbers for grid graphs of arbitrary dimensions. In this paper, we define the density of a \((t,r)\) broadcast, which allows us to provide optimal \((t,r)\) broadcasts on the infinite grid graph for all \(t \geq 2\) and \(r=1,2\), and bound the density of the optimal \((t,3)\) broadcast for all \(t \geq 2\). In addition, we give a family of counterexamples to the conjecture of Blessing et al. that the optimal \((t,r)\) and \((t+1,r+2)\) broadcasts are identical for all \(t \geq 1\) and \(r \geq 1\) on the infinite grid.

Along with Clayton Sanford, I was the Computer Science PhD Student Representative at Columbia University from 2022-2024. We worked to make the department more transparent and accessible to PhD students by building knowledge bases and creating structured channels for feedback to faculty and administration.

With Roland Maio, I coordinated the Emerging Scholars Program at Columbia University from 2019-2022. We worked to broaden the diversity of student perspectives in the department and give CS majors at Columbia the tools to reason ethically about Computer Science.

At Columbia, I focused my outreach work on making the path to graduate education easier to understand and navigate. I spoke as part of the Demystifying the PhD and Demystifying the Dissertation outreach lecture series.

I have participated in undergraduate mentorship as part of Women in Science at Columbia's mentorship program and the Barnard BEARS (Better, Enhance, & Advance Research Series) program. I've also mentored high schoolers in research with Lumiere Education and the Williams College Alumni Mentorship Program.

In 2021-2022, I assisted in organizing the Student Workers of Columbia. Living wages, fair benefits, and discrimination recourses ensure that student workers can do their jobs without facing poverty and harassment. Moreover, they make work in academia accessible to those with fewer outside resources.

I'm a proud participant in the ongoing struggle to create a just, antiracist Computer Science department at Columbia. In this context, I have worked on expanded outreach to broaden the pool of research applicants and improving admissions practices and oversight. (If you're interested in recieving feedback on your personal statement for a PhD program, check out CUCS' Pre-Submission Application Review program.)

Along with Clayton Sanford, I organized Columbia's first two annual theory student retreats! I'm now an organizer emeritus.